Hello there today i came up with another sorting technique. So let us understand it in an easy way with an example.
Overview of Heap Sort
It is an in-place algorithm which means no extra memory space is required to store the sorted array as we have seen in Merge Sort. The list can be divided into two parts one is heap(unsorted) and the second is sorted list.
Performance of Heap Sort
It’s Best, Worst and Average Case Performance are all same i.e., —– O(n log n)
Before I tell you how it works just take a look of some terms, that we are going to use:
Binary Tree/ Heap
It is a tree which have root on the top and leaves at bottom. Binary implies that a parent can only have maximum of two children. Left child and Right child. Elements are termed as Nodes.
This this diagram for better understanding
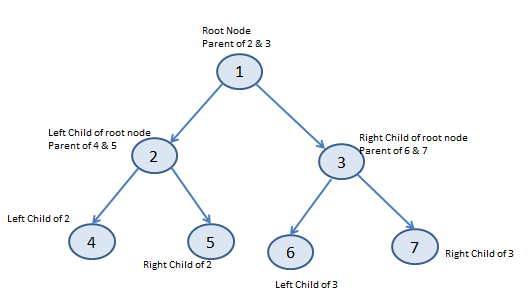
Max Heap
It means that the parent should be greater than both of its child Nodes.
How Heap Sort works
With the help of unsorted array, a heap is created (you can call it as a binary tree). Then it is converted to max heap. Due to this the largest element will come at the root node Then finally it is extracted from the heap/unsorted part to the sorted part of the list. Hence heap is reduced by one Node. Don’t worry guys if you don’t understood it go through the example, things will get clearer.
Step By Step Example
Remember 3 steps for its working:
1. Create a heap from the unsorted list.
2. Convert it to max heap
3. Swap – root node with the last node, and then remove the last node.
Now Take an example of unsorted array having 9 elements.
![]()
Step 1: Create Heap
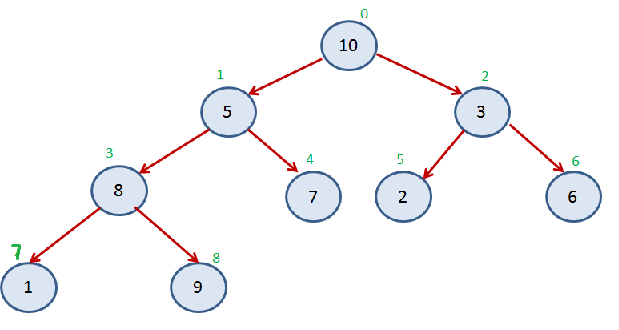
Step 2: Max Heap
Starting from the bottom parent, convert the heap into max heap. By swapping the parent with its greater child if parent is less than its child. See the diagram how we are converting follow steps 1,2,3 written in green. Orange arrows shows the swapping of nodes.
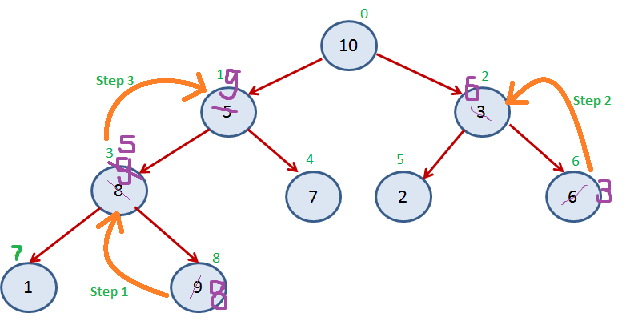
Step 3: Swap root with last node & Remove last node
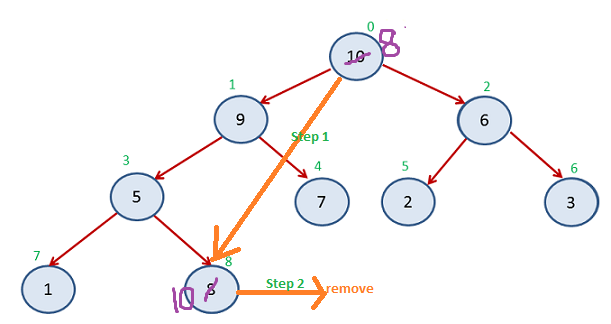
So 1 element is reached to its correct position –

Note : Elements from Index 0 to 7 are unsorted part(heap) and index is in sorted part of the array.
Now As I said Repeat Step 2 and 3 till one Element left.
Again Step 2
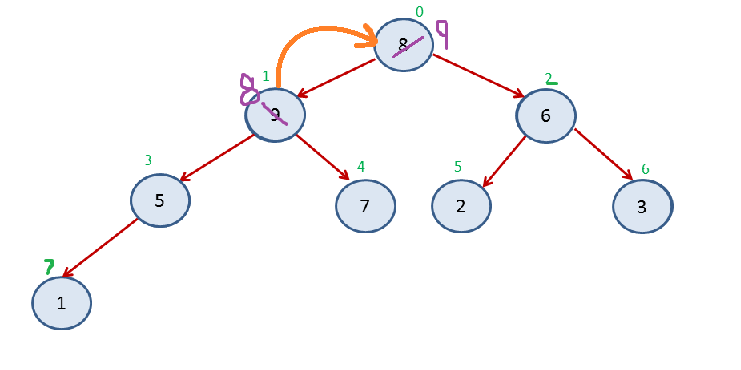
Again Step 3
Now 1 more element from heap get sorted.

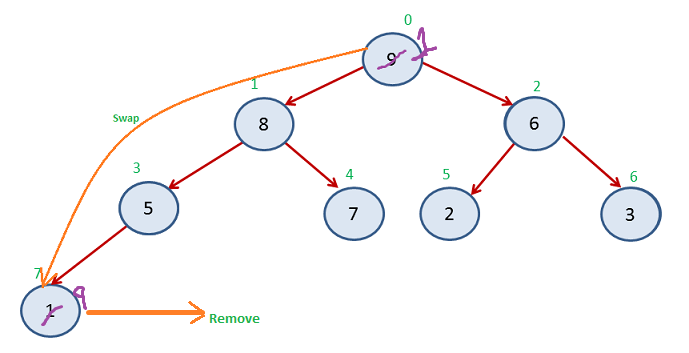
Again Step 2
Again Step 3
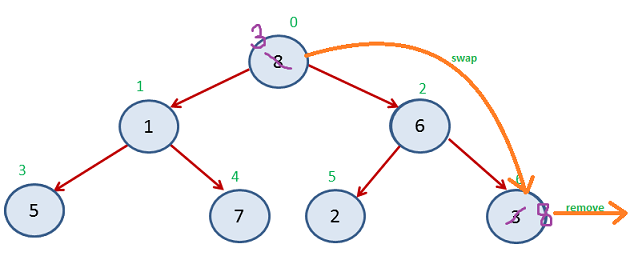
Now Index 0-5 (unsorted heap) and Index 6-8 sorted

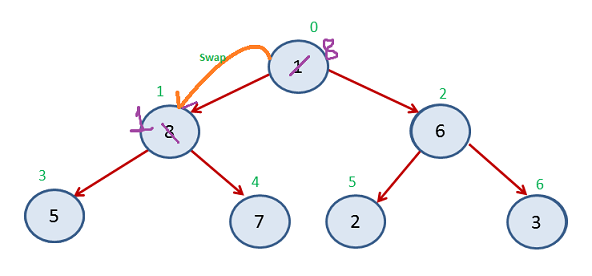
Again Step 2
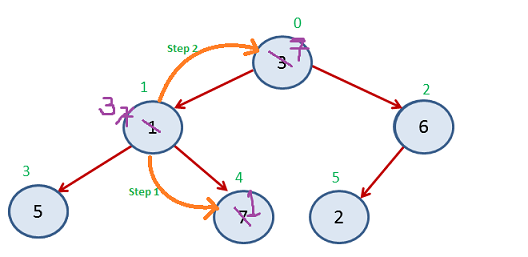
Again Step 3
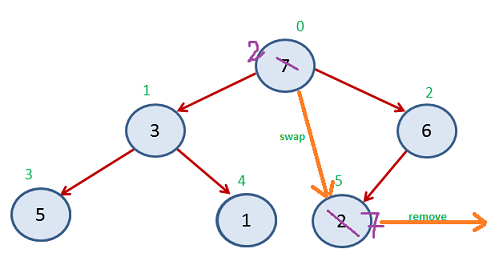
Index 0-4 in heap/ unsorted and Index 5-8 sorted

Again Step 2
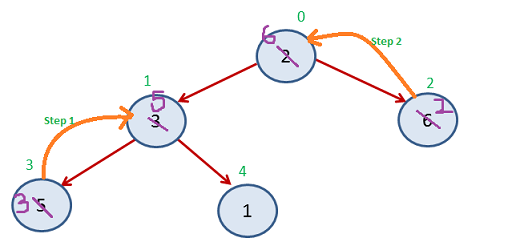
Again Step 3
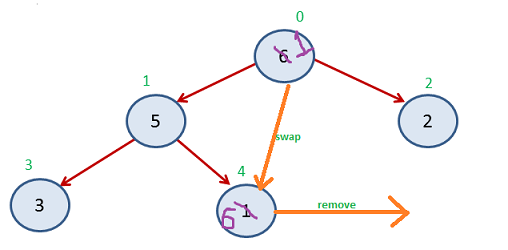
Now Index 0-3 left unsorted and Index 4-8 get sorted

Again Step 2
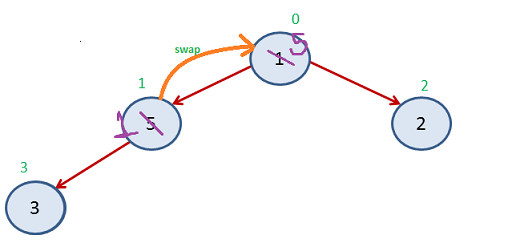
Again Step 3
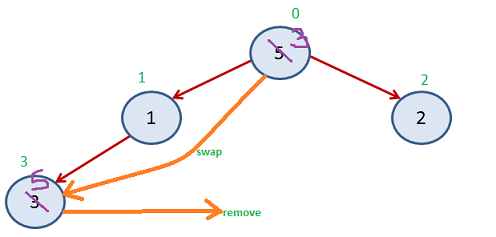
Now Index 3-8 get sorted

Again Step 2
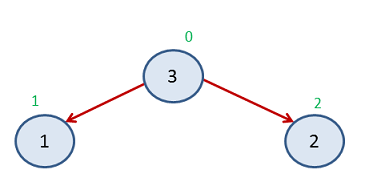
It is already a Max heap
Again Step 3
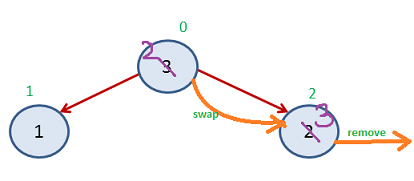
Now Index 0-1 left unsorted and Index 2-8 is sorted

Again Step 2
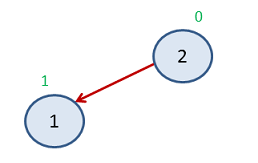
It is already a Max heap
Again Step 3
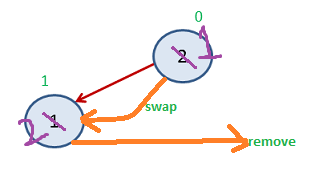
Now Index 1-8 get sorted and only 1 element left in heap

So simply that would get inserted in sorted list

So we have seen how heap sorting works which is as easy as a pie.
Thank You. I hope you enjoyed reading