Insertion in a BST (Binary Search Tree) means you are inserting a new node / element to the Binary Search Tree and by doing so the keys should remain properly ordered.
I assume you know about Binary Search Tree. If not Read it from here.
Now let’s take an example and insert nodes in BST
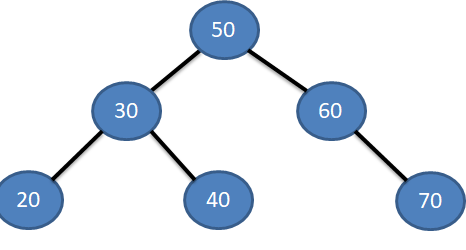
50 30 60 20 40 70
Lets us start with 50 , it is first element hence becomes our root Node.

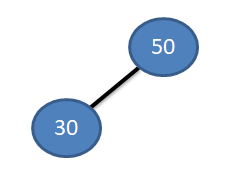
Now next element is 30, which is smaller than 50. So it will become the left child of the Node.
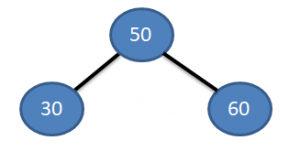
Now turn for the third element 60. As 60 > 50 … therefore it will be inserted as the right child of the Node.
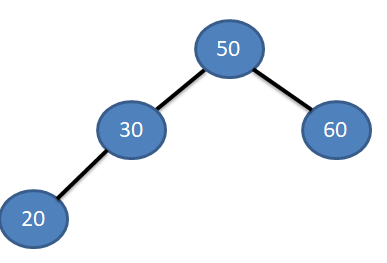
Next element in the list is 20. And 20 < 50. So move to the left. Root node already have a left child (30) , So now compare 20 with 30. You will find that 20 < 30 therefore we will move to its left and As the place for left child is vacant here , the new node (20) is inserted here.
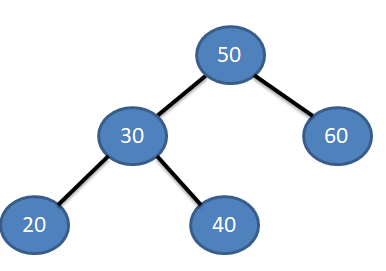
Next element to be inserted is 40. So here also we start comparing from the root node and look out for its place to insert. Starting from root node, 50 (40<50). Then moving towards left (40>30). Then going towards right, it dont have right child so new node inserted here.
Then our last element 70. Follow the same process and it will be inserted as right child of node 60. See below.
Now as you understood the whole concept, So take a look on the Algo of inserting a new node in Binary Search Tree (BST)
Algorithm
- Allocate memory to new node, Assign value and make left / right child of new node = null.
- Locate parent of new node.
- currentNode = root
- parent = null
- Repeat until currentNode =null
- If newNode < currentNode, then currentNode = currentNode = currentNode's left child
- If newNode > currentNode, then currentNode = currentNode = currentNode’s right child
- If parent = null (tree empty)
- newNode = root, Exit
- If newNode < parent
- parent’s left child = newNode, Exit
- If newNode > parent
- parent’s right child = newNode, Exit