Binary Tree is a tree which is either empty or consists of a root node together with 2 nodes, each of which in turn forms a binary subtree.
Before going through Binary Tree it is advised to have some basic knowledge of Trees in Data Structure. Click to read about Trees in Data Structure.
Empty Tree

Binary Tree
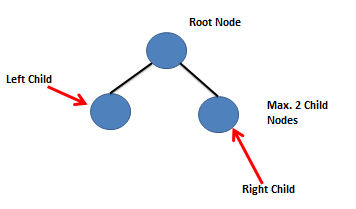
Types of Binary Trees
1. Strictly Binary Tree
A Binary Tree is strictly binary tree if every node except the leaf nodes have non-empty left and right children.
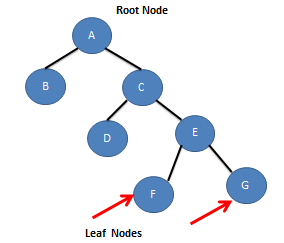
2. Full Binary Tree
A binary tree of Depth d is said to be a full Binary tree if it has 2^d -1 nodes
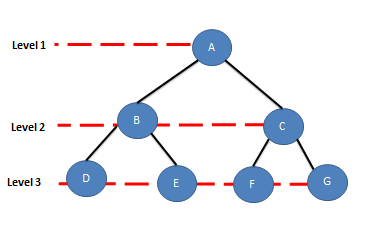
depth = 3
nodes = 2^3-1 = 7
3. Complete Binary Tree
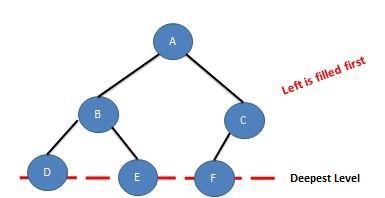
A binary tree in which all levels except possibly the deepest level are completely filled and at the deepest level all nodes are as far as left as possible. i.e., left child is filled first.
Implementation of Binary Tree – How you represent Binary Tree in Memory
1. Array
2. Linked List
Figure 1:
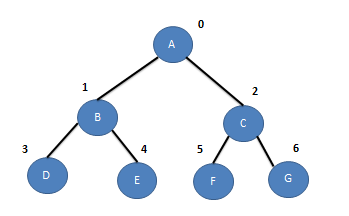
Array
Nodes in a binary tree is numbered in a very easy and natural way starting from root, level by level , left to right. Numbers starts from 0, these numbers represent the indexes of the array.
See figure below :

Array with reference to figure 1.
Some formulas you can use :
Parent of i = index(i-1)/2 where 0<i<n-1
You can also find the left and right child of a node
Left Child of i = index 2i+1 , if (2i+1) > n-1 => it has no left child
Right Child of i = index 2i+2 , if (2i+2) > n-1 => it has no right child
Linked List
While implementing Binary Tree as Linked List, if left/right child of any node doesn’t exist then the points to Null.
See figure
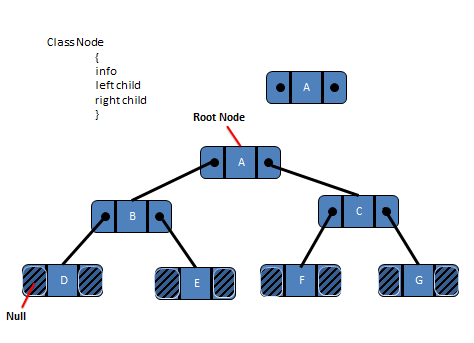
Linked List with reference to Figure 1.